How To Divide By Zero

Normally, I like to discuss how to make science fiction a reality. But this time, I’m going to talk about a piece of fiction which has long been regarded as science reality: the myth that one simply cannot divide by zero. There are those who believe that if one could actually divide by zero, bad things would happen. It could rip a hole in the space-time continuum! It could cause the very fabric of the universe to break down on the subatomic level! It could unleash a horde of zombie clown cockroaches with machine guns hellbent on forcing everyone to polka! Or worst of all, it might cause Yoko Ono to release another album!!!

This is something I have written about elsewhere. This, however, is an extended version which will address concerns I’ve run into.

My hope is that by the time you finish this article, you will see that such a notion is clearly wrong. The solution is very simple, a correction of a logical error. But in order to fully understand how to divide by zero, we first need to look at what division is.

How To Divide

To understand zero division, we need to go back to the very basics. Division is, quite simply, evenly splitting up a given quantity among a given number of locations. If you want to split up forty apples into five baskets, you would put eight apples in each basket. Simple enough: just multiplication in reverse.

But what if the given quantity doesn’t split up evenly? Let’s say you have forty-two apples and five baskets. You would still put eight apples in each basket, but you would have two left over, a remainder (42 / 5 = 8 R 2). Still rather bloody simple. It’s the same thing as taught in elementary school.

The Perceived Problems

There are a few issues which experts have with dividing by zero. It’s these little things which keep them from becoming believers in zero division. I’ll just briefly talk about a few.

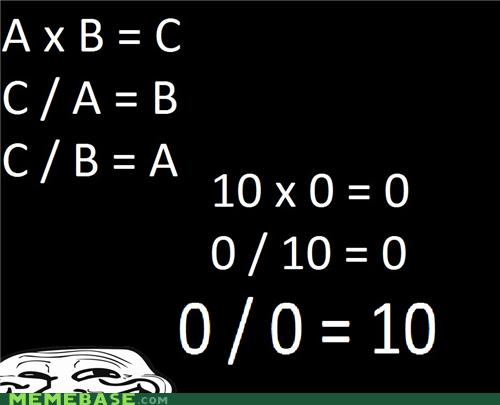
The first is the Converse Function Problem. This is in regard to those who think that anything divided by zero should be zero.  The problem is that it can’t multiply the other way. For instance, eight divided by zero is zero, but zero times zero is most definitely not eight. A valid equation should be able to work in both directions, the converse function serving as a type of proof. Any equations which can’t do that belong in a landfill, in a desert, or on MSNBC. That way nobody will pay it any mind.

Secondly, there is the algebraic error. The assertion is that, if 0 x 1 = 0 and 0 x 2 = 0, then 0 x 1 = 0 x 2. Then we get rid of the zeroes with the expression 0/0 x 1 = 0/0 x 2.  The result is 1 = 2. The problem with this is that it has no real-world application. In the real world, if you have one row and zero columns one place and two rows with zero columns another place, you still have nothing. Looking at nothing and trying to figure out how many rows of nothing there are still results in nothing. Anything which doesn’t apply in the real world is nothing more than a mathematical curiosity. When we see the actual method of zero division, a real-world answer will become clear.

Then there are those who believe dividing by zero results in infinity. There are different places where this answer shows up. Most, I believe, are based on using zero division inappropriately. I think the main issue is treating of zero space as infinite compression. Computers and calculators (and other math-solving electronics) have this error built in. They try to set everything as a decimal equivalent which doesn’t always work. In theory, trying to put a quantity into a space which is, in effect, infinitely compressed (at zero, it can’t be compressed any further) causes the quantity to become infinitely dense.

There are two problems here. One is the idea of infinite. Infinite what? Infinite mass would indicate containing all mass in the universe and then some. Infinite means “without end”. I remember one time when I was about 6 or 7 years old I tried to think about “forever” and “infinity”. I nearly had a panic attack!

The other problem is a biggie. It’s the idea of zero space. You can compress something as far as you want, as long as it doesn’t reach zero. When it reaches zero, it no longer occupies space. If something doesn’t occupy space, it doesn’t exist! That, ladies and gentlemen, is Physics 101.

Handley’s Law of Zero Division

Therein lies the problem. What if you have a quantity to divide and no place to divide them into? Let’s go back to the basics of what division is. Consider the apples in the baskets. Forty apples divide evenly, but forty-two leaves a remainder of two. But what if the baskets can’t be found? If the target containers are non-existent, then the amount in each basket is zero, with a remainder of forty-two, or 42/0 = 0 R 42. If containment does not exist, then the quantity isn’t contained.

Imagine there’s twenty kids going outside to play football at recess. (It doesn’t matter if it’s American football or international football/soccer, just that they’re playing football. Now don’t pick nits.) We can assume that there will end up being two teams with ten kids on each team. But before the team captains and players are chosen, how many are on each team? There are twenty players to play and neither team has any players yet. So twenty players divided among the teams which currently have players (zero) gives us the number of players on each team (zero, with a remainder of twenty). All dividing by zero tells us is that the quantity still exists, just not where one is looking for it.

So I present to you Handley’s Law of Zero Division: x/0 = 0 R x . The converse equation, or proof, is NOT “0 x 0 = x” just as the apples in baskets is not 5 x 8 = 42. The apple and basket equation would be 2 + (5 x 8) = 42. By the same token, the converse of the zero division equation would be x + (0 x 0) = x .

I know what some of you are thinking. How can it be division if the quantity isn’t being divided? My response is simple. It doesn’t matter if a quantity is uncontained or contained in a single location, neither splits up the quantity. But division by one is still acceptable, is it not?

So there you have it, the proper method of dividing by zero. Impress your friends, and annoy your math professors.